|
|
|
This page is about my theory of superativity.
It is a form of math displaying the effectiveness of a movement from a
certain point with height and distance. In other terms, both the
maximum height and the total distance from the point. In superativity,
we use the term nihillian point meaning "zero point." I guess that
leads me into telling you the etymology of the words used: Superativity
comes from the Latin word superarus, meaning "to distance" and nihillian
comes from the Latin word nihil, meaning "zero."
If we are to calculate this value, we must look
into two formulas. First, we'll talk about the simpler formula:
The superative equals the absolute value of the maximum height increased by the total distance.
In other words:
S= Superative, h= maximum height or maximum depth, d= total distance.
S= h + d
So if we find the absolute value of the maximum height and then add it to the total distance we get the superative! Here is a sample problem:
S= 34 +56
S= 34 + 56
S= 90
The superative is 90. That was very simple. Let's look at the unknown variable being on the side with the h and the d:
98= h + 43
-43 -43
55= h
h= 55
Was that simple or what? Now, you may or not be asking, what about if the line goes one maximum height from the nihillian point and then slopes back to the other side? We find the average of both maximum heights with the downward slope equaling negative. Before I thought this new way up, I decided to add both heights. However, I decided that because this depends mainly on gravity you will need to average it out to show how effective the lift was. You may be wondering why I use the term "effectiveness." It is because you are seeing how well the lift it was from gravity was and if it went below the nihillian point you see how incompetent the lift was. I will now give you the formula:
The superative equals the mean of the maximum height and the maximum
depth increased by the total distance.
S= Superative, h= maximum height, m= maximum depth, d= total distance.
S= (h - |m|)/2 + d
This is a little bit different than the former equation, let me show you an example:
S= [55 -|23|]/2 + 76
S= 32/2 + 76
S= 16 + 76
S= 92
The superative is 92. That was a little more
difficult, wasn't it? Well, we're now going to go into graphs and
word problems! If you hate math, you'll probably feel your stomach
churn! But if you hate math, then why are you here? Let us
look at what the layout of the graph is:
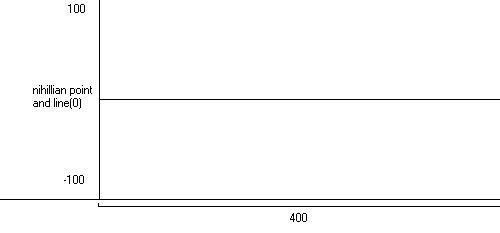
On the left column are height measurents of graph,
with the center being the nihillian point and the layout for the nihillian
line. The top and bottom are the distances from the nihillian point
in height. Let's look at it going to the right, we see a long line
going to the east, the bottom says the total distance from the nihillian
point to the end. If you have a GIF editor, you can use my chart
for your own use of superativity. There is a quick little guide on
it near the bottom of the page.
Let's put some equations on it!
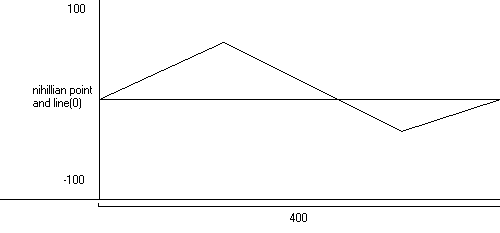
You should know how to solve this. The maximum height is 57, the maximum depth is 32 and the total distance is 400:
S= (57 - |32|)/2 + 400
S= 25/2 + 400
S= 12.5 + 400
S= 412.5 or 412 1/2
The superative is 412.5. You're probably thinking(Most likely not!) about, "What about if you want to solve for something else, maybe like h or m?" Well, I have worked out 2 new formulas just for that! They are:
h= 2(S - d) + |m|
±m= 2(d - S) + h
That is all for now! Meanwhile, check my guide for tips on putting your very own equations on my graph!
1) Right-click on the picture and press "Save Image As..." and save the file to the hard drive.
2) Open it up, use the zoom control to zoom in.
3) Try to place something like a dot, then imagine a line going from it to your second dot(Which the first should be on the top side of the nihillian line and the second should be on the bottom.).
4) For starters, make the line go to all the way to the end(400). If not, take the number(The x-coordinate or domain, you can see it on the status bar, the one that tells you the coordinates of your mouse.) then subtract 99 from it, that'll be your distance.
5) Now, for the maximum height(The one going UP^ over the nihillian line.), add 1 to the y-coordinate or range then subtract it from 100 and that'll be your maximum height. Now, for the maximum depth! Find the point, look at the y-coordinate or range and then subtract 99 from it and that'll be your maximum depth!
6) Now, draw lines to connect it and you'll be ready!
su-per-a-tiv-i-ty(soo-per-uh-tiv-i-tee)(p. superativities) n. A theory stating to find out the effectiveness of a movement from a certain point, the nihillian point, which is, in simple means, the sum of the maximum height or depth and the total distance.
su-per-a-tive(soo-per-uh-tiv)(p. superatives) n. The sum of a maximum height or depth and the total distance, or the mean of a maximum height and a maximum depth plus the total distance.
ni-hill-ian(ni-hil-yan or ee-an) adj. Of or having to do with zero.
Do you accept this or not?
Go back to the main page.